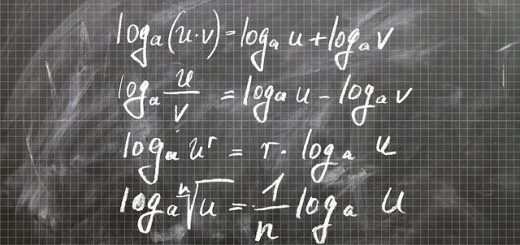Special Case of Vedic Math Derived Base Multiplication

Today we’ll discuss a special case of multiplication using derived base method of Vedic Math. To do this we’ll take the example of :

72 x 88 OR 72 * 88 (to be solved later in this post)

Now this is a type of question that can be solved using the Sub-Multiples Technique of the Base Method of Multiplication. For eg.

52 x 48

52 | +2 (Base taken as 50 and the difference +2 is written separately)

48 | -2 (Base taken as 50 and the difference -2 is written separately)

————-

50 * 5 | -4 (On the LHS, Cross addition or Cross subtraction is done i.e. 52 – 2 OR 48+2. Post this the result 50 on LHS is multiplied by 5 as the base of 50 is a derived base from 10*5=50; this process should be remembered as a rule)

250 | -4 (On the RHS, we have -4 which is the product of +2 and -2)

2496 (Since there was -4 on RHS, we took a carry from 250 making the LHS 249 while doing 10 -4 with the carry from the 10s place to give the final result of 2496)

Special Case: 72 x 88

Following the above rule with base a 80 derived from 10 x 8 =80, we get:

72 | -8

88 | +8

80 | – 64 (LHS is 72+8=80; And RHS is [-8]*[+8] = [-64])

Now to accommodate the derived base of 10*8 = 80, we’ll multiply 80 by 8 on LHS

640 | -64

Now, the no. of digits on the RHS can only be the number of zeros on the base so it should have only 1 digit. Thus, technically the place value of 4 in 640 will be the Hundreds value (counting from RHS assuming it should have only one digit —> ones as in whatever # comes in RHS, tens as 0 and hundreds as 4 and thousands as 6 in LHS)

Now since -64 will require a carry from hundreds place (and 0 will be added to the result of RHS’s tens place value), we take a carry from the hundreds place and thus on RHS we get 100 -64 = 36. Now this 3 in the tens place will be added to 0 in the tens place. Thus, our final answer is 6336.